Applications

A comparison of Monte Carlo and Quasi-Monte Carlo
methods for option pricing

In this study we consider European call options. Computation of other options and risk measures (Gammas) are presented here and here. European call option provides the holder of the option with the right to buy the underlying asset by a certain date for a given price known as the strike price. The date in the contract is known as the maturity. The payoff function is the following:

Here

ST is the asset price at the maturity, K is the strike price.

In a risk-neutral environment, the value of a derivative is the discounted value of its expected terminal date cash flow:

Monte Carlo simulation approximates the expectation of the derivative's terminal cash flows with an arithmetic average of the cash flows taken over a finite number of simulated price paths:

Numerical results and discussion

Assumptions:

Asset, t=0	100
Volatility	20.00%
Int. rate	5.00%
Strike	100
Expiry	0.5 [years]
Black-Scholes Value: 6.88

Payoff:

Call(Expiry) =
exp(-5% * 0.5) * max(AssetPrice – 100,0)

Simulation Parameters:

Time-Step size: 0.01 years

Number of time steps: 50

Number of paths: 6,000

Fig. 1: Price of European Call versus the number of paths obtained using MC and QMC methods with Standard and Brownian Bridge approximations.

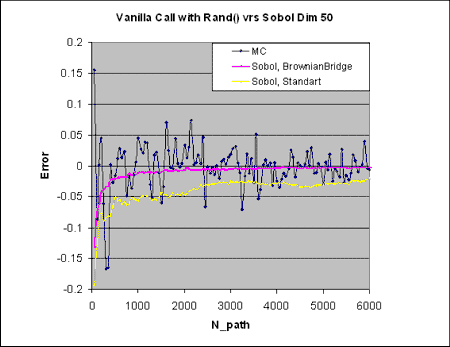
Fig. 2: Relative error versus the number of paths for MC and QMC methods with Standard and Brownian Bridge approximations.

Fig. 3: Log-log plot of the absolute value of the relative error versus the number of paths for QMC methods with Standard and Brownian Bridge approximations.

Results show superior performance of the QMC approach based on SobolSeq with the Brownian Bridge approximation. The convergence rate for the Brownian Bridge approximation decreases as 1/N0.82, while for the Standard approximation this rate is only 1/N0.4.

Broda's generator was used for simulation.